Implementing Bitonic Merge Sort in Vulkan Compute
A bitonic sorting network lays out a sequence of compare-and swap operations that, when applied to an array of sortable elements, sorts these elements.
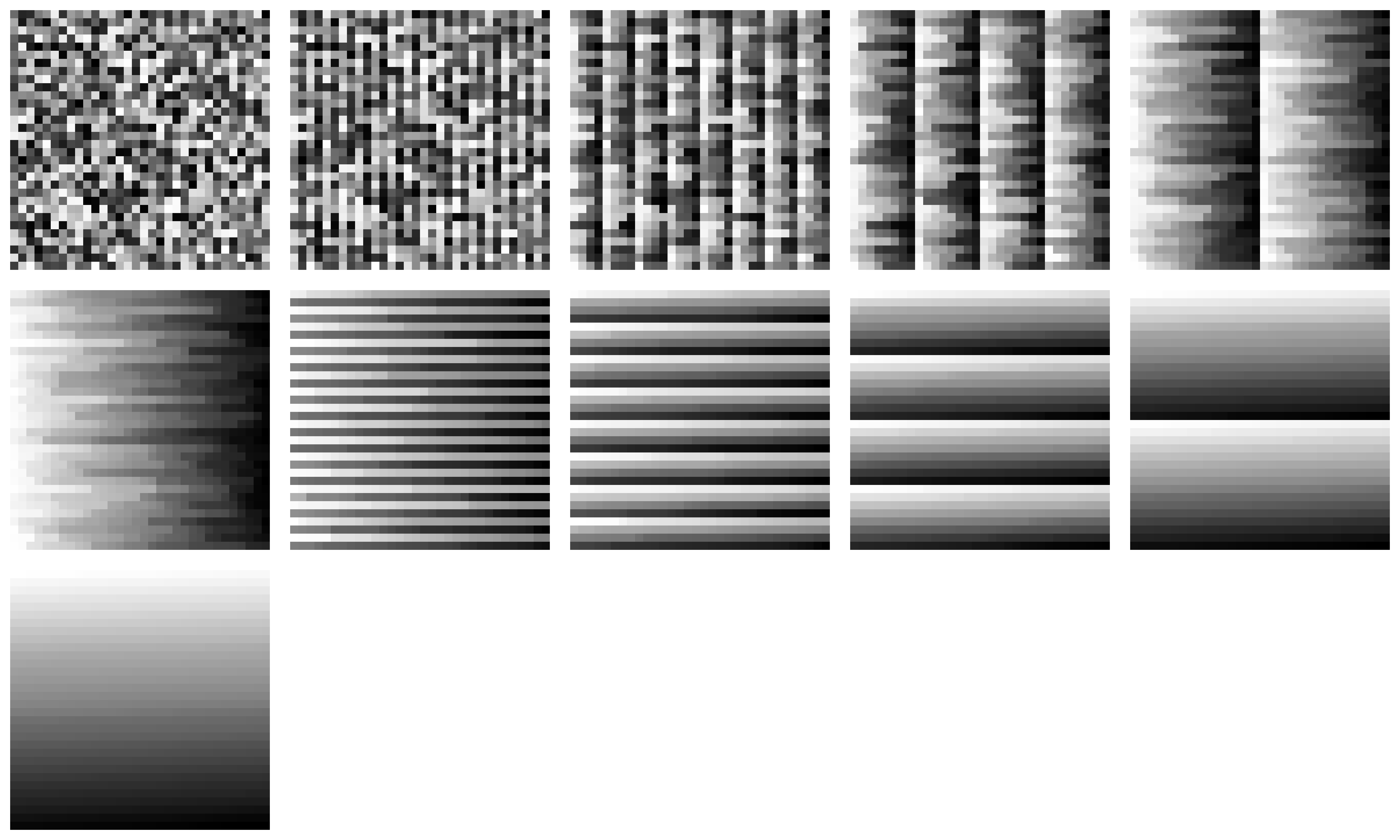
The pixels in the final square are sorted by brightness, left-to-right and top-to-bottom.
Why Bitonic Merge Sort?
The beauty of this algorithm is that it maps really well onto parallel hardware, such as a GPU, where it has constant and relatively low performance complexity \( O(\log^2(n)) \). That is to say: It’s quite fast. The implementation I’m discussing here was able to sort 1M random ints in 4ms. Compared to the 40ms I measured for C++’s std::sort, that’s a 10x speedup! On top of that, for a given number of sortable elements, it will always take the same amount of time to complete.
When the algorithm executes, each worker thread performs one single operation for every pair of sortable elements: compare-and-swap. But how to choose the correct pairings for sortable elements? This is where the algorithm’s complexity is buried.
Constructing a Bitonic Sorting Network
First, let’s look at a diagram of a relatively small sorting network, say, for 16 sortable elements. The diagram is for the alternative representation of a bitonic sorting network, as I found it on wikipedia. I prefer this version because it is slightly simpler: all worker threads use the same direction for their compare-and-swap operations.

Fig.1: Sorting diagram for 16 sortable elements
Horizontal lines represent array indices into our array of sortable elements, each vertical line represents one worker thread performing a compare-and-swap operation.
In the diagram, each worker thread is drawn as a vertical line, with the start- and endpoints marking the indices of the current pair of sortable elements. All coloured blocks which are in the same column form a step, wich can be executed in parallel. We can see from the diagram that the number of threads per step is constant, and that it is always n/2, with n being the number of sortable elements.
Before we proceed to figuring out sort index pairs for each worker thread based on each thread’s execution step and thread number, lets take a step back, look at the diagram through squinted eyes and see if some patters emerge if we group similar looking blocks together.
We can point out some macro patterns:
- Green block: doubles in height until it reaches total number of elements. Let’s call such a block flip
- Yellow block: after each green block, there is a cascade of yellow blocks, each half the previous height, until its height spans only two sortable elements. Let’s call such a block disperse
- Blocks are periodic within their column.
We can write the following pseudo-code:
|
|
Look at inner patterns:
Looking at the diagram again, we see that each of the two block types, green and yellow, follow distinct patterns for how each worker thread grabs pairs of sortable elements:

h of a yellow or green block.
We can therefore split the problem in two:
- Find rule to calculate pairs for green (“flip”) block based on height
h. - Find rule to calculate pairs for yellow (“disperse”) block based on height
h.
Index pairs for “flip” (green) blocks
Let’s enumerate sortable element index pairs from our green blocks, and label them \( T_{0\dots t} \), where \( t \) represents the worker thread index to which a sortable element index pair is assigned to:
\( \begin{align*} h = 2 &: T_0 [0:1] \\ h = 4 &: T_0 [0:3], T_1[1:2]\\ h = 8 &: T_0 [0:7], T_1 [1:6], T_2 [2:5], T_3 [3:4]\\ \end{align*} \)
We see that we can form pairs of indices based on the following rule:
\( T_t = [ t : h-t-1], \text{ for } t = 0,\dots,h/2 \)
Index pairs for “disperse” (yellow) blocks
Similarly, if we enumerate index pairs for yellow blocks we get
\( \begin{align*} h = 2 &: T_0 [0:1] \\ h = 4 &: T_0 [0:2], T_1[1:3]\\ h = 8 &: T_0 [0:4], T_1 [1:5], T_2 [2:6], T_3 [3:7]\\ \end{align*} \)
We see that we can form pairs of indices based on the following rule:
\( T_t = [t : t + h/2], \text{ for } t = 0,\dots,h/2 \)
Rules for rows of blocks
Now, let’s look at the diagram again.

Our original diagram
We notice that both green and yellow blocks repeat vertically until they fill out the full height of their column. We can model this repetition as a combination of modulo (the pattern is the same within a block) and an integer-division based offset.
As a first step, we make sure both rules for green and yellow blocks are contained within their respective height, \( h \). Note that we define these rules now for the total number of sortable elements, \( n \) instead of the earlier \( h \). Instead of using \( t \) “unbounded”, we introduce a new term around \( t \):
\( T_t = [ q + (t\bmod \frac{h}{2}) : q + h-(t \bmod \frac{h}{2})-1], \text{ for } t = 0,\dots,n/2 \)
\( T_t = [ q + (t \bmod \frac{h}{2}) : q + (t \bmod \frac{h}{2}) + \frac{h}{2}], \text{ for } t = 0,\dots,n/2 \)
What does the new term \( (t \bmod \frac{h}{2}) \) do? It limits the output for the term for any given \( t \) to \( 0,\dots,h/2 \), something you will recognise as a condition for our earlier rules.
You will also have noted that both rules introduced a new variable \( q \), which represents the offset. We can express \( q \) fully as a function of \( h \) and \( t \):
\( q = (\lfloor{ \frac{2t}{h} }) * h \)
In pseudo-code, this translates to:
|
|
Let’s make a first POC!
In order to test these little formulas, and becasue I thought it would generate some nice visuals, I wrote a little C program which, when given a count of sortable elements, prints a diagram, and index pairs for each step of the resulting sorting network.
Implementing this as a Vulkan compute shader
Now that we have a reliable and tested method to generate index pairs, we can take a stab at implementing the algorithm using Vulkan Compute.
In Vulkan, compute tasks require us to bind a compute pipeline - which is thankfully very simple and takes a single compute shader. We’ll get to the code for the compute shader in a little bit, but for now, let’s look at what we need to specify in order to dispatch a compute command:
|
|
We need to find the group counts in x, y, and z dimension for our dispatch command. Since we want each compute command to execute one step of our bitonic sorting grid, let’s stick to a one-dimensional invocation: I’m setting groupCountY = 1 and groupCountZ = 1, since these values must be at minimum 1.
What do we set for groupCountX?
Well, this will depend on the size of our workgroup, and the total number of sortable elements. Let’s say we have \( n=16 \) sortable elements. This means, we will need \( \frac{n}{2} = 8 \) worker threads. Let’s say each workgroup contains 8 worker threads, this means we would need to call our dispatch with a groupCountX of 1.
Every invocation triggers one workgroup of thread workers. In shade code, we can specify how many threads we want to have per work-group, by specifying local_size_x, and in this particular case, we would choose 8.
Naive Bitonic Merge Sort
Now, let’s look at a first stab at a shader implementation for bitonic merge sort:
|
|
Note that in this implementation we’re using shared memory (#L15). This is a pretty important optimisation. Reading and writing from GPU global memory is pretty slow, and it is much faster to keep memory on cache for as much as we can. The closest cache we have at hand on a compute shader is the shared cache, which is shared amongst all threads within a local workgroup.
In our particular case, this means the 8 threads of our workgroup share the same cache, and because the cache is allocated at the size of the total number of sortable elements, n, we can fit all our sortable data into our local workgroup cache.
Why use shader local memory?
Using local memory (that is local workgroup cache) allows us to execute multiple steps of the algorithm on a single compute shader invocation. This is much faster, because once the cache is populated, we can do all the work on local memory, before writing back our results to global GPU memory.
To prevent any data races on our local cache, we issue barrier() instructions whenever we want to make sure that all worker thread writes have completed, before we continue execution. Because we know that each step of the algorithm can execute fully in parallel, we need only to issue barriers after each step, and just before we access global memory.
Know your limits: This won’t scale
The shader above is a working implementation of a bitonic sorting network. It will, alas, not scale, as hardware limits apply. There are two major hardware limits: One is the total volume of worker threads which can be issued per work_group, the other is the total number of bytes which may be used as local cache. Fortunately, we can query these limits via Vulkan.
The relevant hardware limits are: maxComputeSharedMemorySize for the total number bytes used for local workgroup cache, and maxComputeWorkGroupInvocations for the total volume of worker threads for one workgroup.
How can we work around these limits, then?
But this will scale: Bitonic Merge Sort for Arbitrary Power of 2 Sortable Elements
Ideally, we’d like to increase local_size_x to mirror any change in n. To keep things very simple, we’d like our worker thread count \( t = \frac{n}{2} \), so that we could run everything inside of a single workgroup, and always invoke our compute shader with a groupCountX of 1.
But, as we have just established, even GPUs have a limited number of worker threads. Perhaps the best way to adapt to this incovenience is to invoke our compute shaders with a groupCountX > 1, which means we must first see how we can divide the problem into g groups.
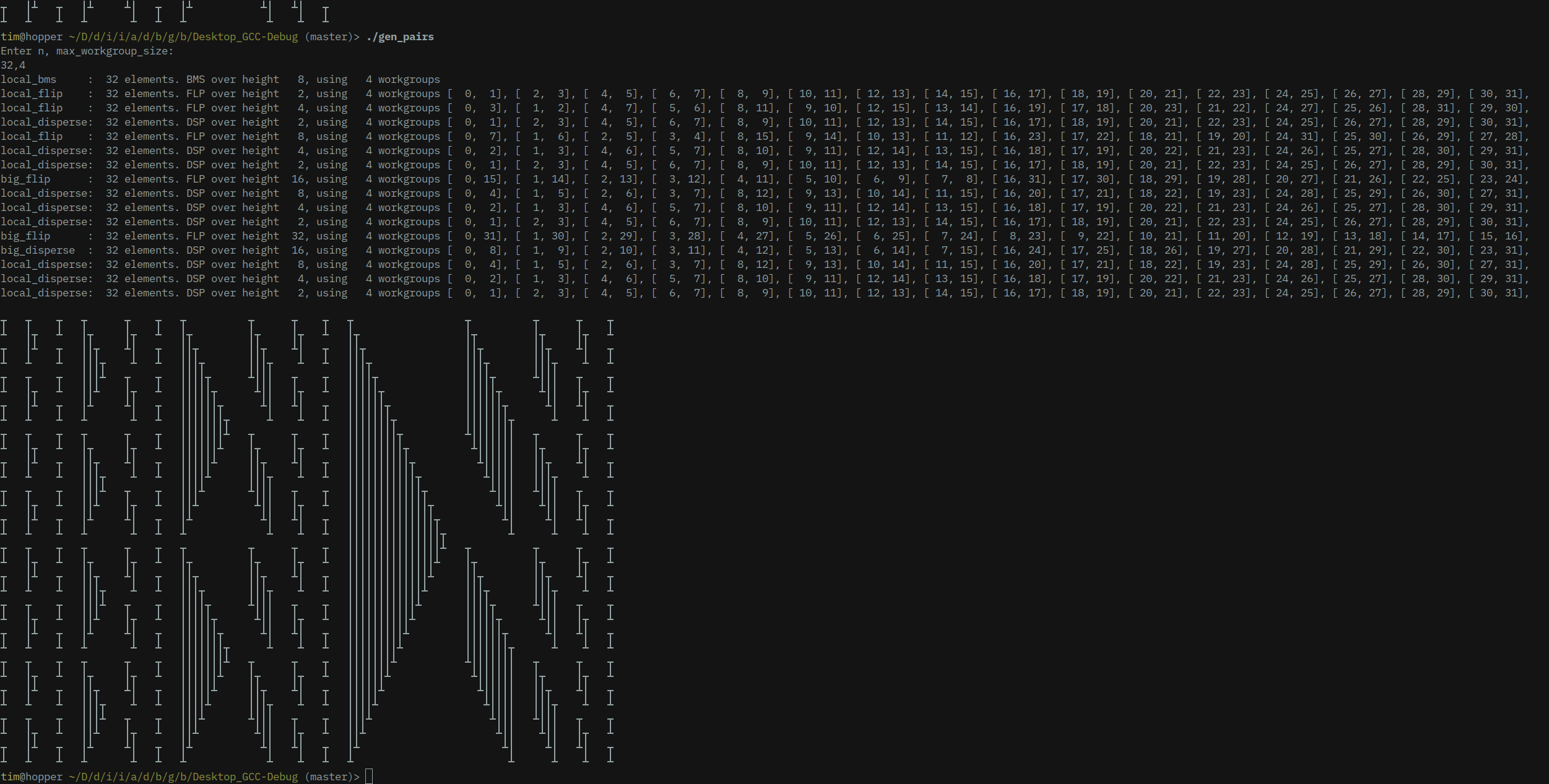
Let’s look at our diagram again. Let’s say we have a number n == 16 of sortable elements, but a maximum group size of 4 thread workers per workgroup. This would split our workload into two lanes (shaded light- and dark blue in the diagram):

Bitonic merge sort network, split over two workgroups (shown as a light- and a dark blue lanes).
Note: Thread workers are shown as vertical lines, with the dark circles marking the first and second parameter they take for their compare-and-swap operations.
We notice the following patterns:
Up to and including step 6, and labelled local_bms in the diagram, no thread worker needs to reach out of their lane, all steps may operate on the local memory of a thread’s workgroup.
Step 7 is special, as compare-and-swap operations reaches across the group’s lane. Let’s label this step big_flip.
In steps 8 - 10, a cascade of disperse operations, all compare-and-swap operations are self-contained within: local_disp.
Not in the diagram, but by extrapolation plausible, is a step where a “disperse” operation reaches over the lane boundary: big_disperse.
Update CPU code to allow large numbers of sortable elements
From the diagram above we have enumerated the following four cases:
- local binary merge sort
- big flip
- local disperse
- big disperse
Before we adapt our shader code to accomodate for these four cases, we must rethink how we organise our CPU code.
|
|
Each call to dispatch() etc. triggers a compute shader dispatch, followed by a compute shader memory barrier. The barrier (lines 30-32 in the following code snippet) is needed to enforce that the previous step has fully completed before the next step of the algorithm begins.
|
|
Adapting Shader indices calculations
In addition to updating out CPU-side code, we also must update our shader code. Our compute shader must provice four different kernels, one each for local binary merge sort, big flip, local disperse, and big disperse. We could write four different shaders, and bind a different pipeline before calling dispatch, but for my proof of concept, I used a uniform parameter and some if-statements on the shader to invoke the chosen algorithm. Since, for each dispatch, all thread workers are running the same code path, there should not be any significant penalty for using an if-statement in this case.
Now, take a closer at how we need to update our shader code so that we can sort arbitrary power-of-two sized arrays.
Near compare-and-swaps: Local indices + offset
With local_disperse and local_bms operations, our workgroups do not reach out of their lane. Therefore we can keep calculating offsets based on local t and h as outlined above. All we have to do is to apply a constant offset which corresponds to the lane we’re on, before we pull data to local memory, on which these algorithms operate. This offset r is calculated based on the height of a lane, multiplied by its index:
\( r = 2 * workgroup\_size\_x * group\_id\_x \)
At the end of local_disperse and local_bms operations, we must make sure to apply the offset again, when we write our locally stored results back to global memory.
Far compare-and-swaps: Global indices + splitting
For workgroups which reach out of their lane, we can’t use local memory, and all index addresses must be global.
Let’s look at the diagram again.

workgroup_size_x * 2 == 8
How do we enforce that any sortable element is only ever touched by a single worker thread from any workgroups invoked during such a big_[disperse|flip] step?
We don’t operate on local \( t \), but calculate global \( t' \) for each worker thread. This applies for big_flip, and big_disperse:
\( t' = workgroup\_id\_x * workgroup\_size\_x + local\_id\_x \)
This gives us an updated rule for big_flip:
\( T_t = [ q + (t'\bmod \frac{h}{2}) : q + h-(t' \bmod \frac{h}{2})-1], \text{ for } t' = 0,\dots,n/2 \)
… and for big_disperse:
\( T_t = [ q + (t' \bmod \frac{h}{2}) : q + (t' \bmod \frac{h}{2}) + \frac{h}{2}], \text{ for } t' = 0,\dots,n/2 \)
Note that the global offset \( q \) is still calculated as before, that is:
\( q = \lfloor{ (\frac{2t'}{h}) } * h \)
Updated shader code
The last step is to put this all together. Which gives us the following updated shader code:
|
|
Find a working example of this code in Island’s examples directory

Summary
This post describes how to implement bitonic merge sort in parallel GPU code, and the required CPU code to host and organise the dispatch of compute kernels. It was written to deepen my understanding, and to please a reader casually interested in GPU programming. If you’ve made it this far, thank you, you have been most indulgent:)
What I learned so far
Implementing an algorithm on the GPU can be daunting, especially as limited debugging tools made it challenging to test whether the indices I calculated, for example, were correct. Writing a little C program which would generate and visualize indices proved invaluable, as it gave me a reliable method to test my code without having to run GPU debuggers, and ponder endless tables of numbers.
Speaking of which, I recommend generating visual debug outputs if you can: A graphical representation of your data is about 100x as readable as a tabular or textual representation, and it’s much easier to discover bugs and patterns even at the first glance.
Writing this article helped me to deepen my understanding, and the process of having to explain the index calculations led me to simplify some rules which I was overthinking in the first working draft. It seems that conceptual elegance comes more easily when, after time, sharp edges are worn down by experience.
I’ve implemented this algorithm while participating in the Winter2'21 batch at the Recurse Center. Somebody there, I wish I could remember who, said a sentence which resonated quite deeply with me, and which I tried to apply whenever I got stuck implementing this algorithm:
When in doubt, write code.
Thank You
Special thanks go to fellow Recurser Julia Evans who gave me feedback on an earlier version of this post.
Tagged:
RSS:
Find out first about new posts by subscribing to the RSS Feed
Further Posts:
- Colour Emulsion Simulations
- Watercolours Experiments
- Vulkan Video Decode: First Frames
- C++20 Coroutines Driving a Job System
- Vulkan Render-Queues and how they Sync
- Rendergraphs and how to implement one
- Callbacks and Hot-Reloading Reloaded: Bring your own PLT
- Callbacks and Hot-Reloading: Must JMP through extra hoops
- Love Making Waves
- 2D SDF blobs v.1
- Earth Normal Maps from NASA Elevation Data
- Using ofxPlaylist
- Flat Shading using legacy GLSL on OSX